上海青浦高级中学2018-2019学年度第一学期9月水平测试
高中三年级数学试题
1、填空题
1.集合
则
______.
2.若函数
，则
________.
3.在
的二项展开式中,第四项的系数为__________.
4.某兴趣小组有2名男孩和3名女孩,现从中任选2名学生去参加活动,则恰好选中2名女孩的概率为________.
5.已知某圆锥体的底面半径
沿圆锥体的母线把侧面展开后得到一个圆心角为
的扇形,则该圆锥体的表面积是__________.
6.已知直线
与直线
,记
，则D=0是直线
与直线平行的__________条件.
7.设函数
，若对任意的实数
都成立，则
的最小值为_________.
8.若
满足
,则
的最小值是_______.
9.能说明“若
对任意的
都成立,则在
上是增函数”为假命题的一个函数是_________.
10.已知椭圆
，双曲线
，若双曲线N的两条渐近线与椭圆M的四个交点及椭圆M的两个焦点恰为一个正六边形的顶点,则椭圆M的焦距与长轴长的比值为________.
11.在△ABC中,角A、B、C所对的边分别为
,∠ABC=120°,∠ABC的平分线交AC于
点D,且BD=1,则
的最小值为________.
12.在实数集R中,大家概念的大小关系“＞”为全体实数排了一个“序”。类似地,大家在复数集C上也可以概念一个称为“序”的关系,记为“＞”。概念如下:对于任意两个复数：
当且仅当“
”或“
”且“
”。按上述概念的关系“＞”，给出以下四个命题:
①若
,则
；
②若
，则；
③若,则对于任意；
④对于复数
,若,则
.
其中所有真命题的序号为______________.
2、选择题
13.设集合，则
A.当且仅当
时,
B.对任意实数
时,
C.当且仅当时, D.对任意实数时,
14.在平面直角坐标系中,记为点P
的到直线的距离,当变化时,的最大值为
A.4 B.3 C.2 D.1
15.某四棱锥的三视图如图所示,在此四棱锥的侧面中,直角三角形的个数为
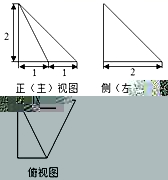
A.1 B.2 C.3 D.4
16.在△ABC中，设是边AB上肯定点,满足
,且对于边AB上一点P,恒有
,则
A.∠ABC=90 B.∠BAC=90° C.AC=BC D.AB=AC
3、解答卷
17.
已知函数
.
求的最小正周期和单调递减区间；
若在区间
上恰好有十个零点,求正数
的最小值。
18.
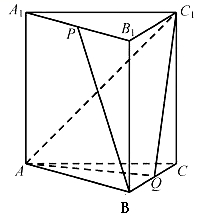
如图,在正三棱柱
中,,点P、Q分别是、BC的中点.
求异面直线BP与所成角的余弦值；
求直线
与平面所成角的正弦值。
19.
已知抛物线
经过点P,过点Q的直线与抛物线C有两个不一样的交点A、B,且直线PA交
轴于M,直线PB交轴于N.
求直线的斜率的取值范围；
设O为原点,
,求证:定值.
20.
数列,概念为数列的一阶差分数列,其中
.
若
,试断是不是是等差数列,并说明理由；
若证明是
等差数列,求数列的通项公式；
对中的数列,是不是存在等差数列},使得
对所有
都成立,若存在,求出数列的通项公式；若没有,请说明理由。
21.当时,若,求和的值；
当
时,设B是A的子集,且满足:对于B中的任意元素,当相同时,是奇数；当不同时,是偶数,求集合B中元素个数的最大值；
给定不小于2的
,设B是A的子集,且满足:对于B中的任意两个不一样的元素，
。写出一个集合B,使其元素个数最多,并说明理由。
